חוקרים השיגו התקדמות משמעותית בגיאומטריה הספקטרלית על ידי הוכחת מקרה מיוחד של השערה של פוליה הקשורה לערכים העצמיים של דיסק. עבודתם, המשלבת אלגנטיות תיאורטית עם יישומים מעשיים פוטנציאליים, מדגישה את הערך האוניברסלי והיופי האמנותי של מחקר מתמטי. קרדיט: twoday.co.il.com
פרופסור ושותפי הפעולה שלו הוכיחו את ההשערה של פוליה לגבי הערכים העצמיים של דיסק, בעיה מסובכת במתמטיקה.
האם ניתן להסיק את צורתו של תוף מהצלילים שהוא משמיע?
זה מסוג השאלות שיוסיף פולטרוביץ', פרופסור במחלקה למתמטיקה וסטטיסטיקה באוניברסיטת מונטריאול, אוהב לשאול. פולטרוביץ' משתמש בגיאומטריה ספקטרלית, ענף במתמטיקה, כדי להבין תופעות פיזיקליות הכוללות התפשטות גלים.
פריצת דרך בהשערות מתמטיות
בקיץ שעבר הוכיחו פולטרוביץ' ומשתפי הפעולה הבינלאומיים שלו – ניקולאי פילונוב, מיכאל לויטין ודיוויד שר – מקרה מיוחד של השערה מפורסמת בגיאומטריה ספקטרלית שנוסחה ב-1954 על ידי המתמטיקאי ההונגרי-אמריקאי המובהק ג'ורג' פוליה.
ההשערה נוגעת להערכת התדרים של תוף עגול או, במונחים מתמטיים, הערכים העצמיים של דיסק.
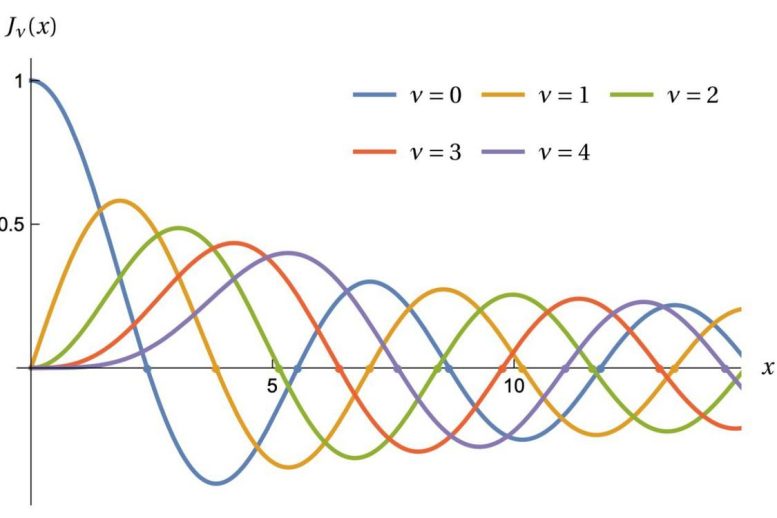
גרף זה מציג פונקציות של Bessel, כאשר הנקודות מתאימות לתדרים של צלילים מתוף עגול. קרדיט: מיכאל לויטין
פוליה עצמו אישר את השערתו ב-1961 לגבי תחומים שמרצפים מישור, כמו משולשים ומלבנים. עד לשנה שעברה, ההשערה הייתה ידועה רק במקרים אלו. הדיסק, למרות פשטותו לכאורה, נותר חמקמק.
"תאר לעצמך רצפה אינסופית מכוסה באריחים מאותה צורה שמשתלבים זה בזה כדי למלא את החלל", אמר פולטרוביץ'. "אפשר לרצף אותו עם ריבועים או משולשים, אבל לא עם דיסקים. דיסק היא למעשה לא צורה טובה לריצוף."
האוניברסליות וההשפעה של המתמטיקה
במאמר שפורסם ביולי 2023 בכתב העת המתמטי Inventiones Mathematicaeהחוקרים מראים כי ההשערה של פוליה נכונה לגבי הדיסק, מקרה שנחשב למאתגר במיוחד.
למרות שהתוצאה שלהם היא בעצם בעלת ערך תיאורטי, לשיטת ההוכחה שלהם יש יישומים במתמטיקה חישובית ובחישוב מספרי. המחברים חוקרים כעת את השדרה הזו.

יוסיף פולטרוביץ'
"בעוד שמתמטיקה היא מדע בסיסי, היא דומה לספורט ולאמנויות במובנים מסוימים", אמר פולטרוביץ'.
"לנסות להוכיח השערה ארוכת שנים זה ספורט. למצוא פתרון אלגנטי זו אמנות. ובמקרים רבים תגליות מתמטיות יפות מתבררות כמועילות – אתה רק צריך למצוא את היישום הנכון."

